DCT Implementation in C# (DCT of Image)
4.50/5 (12 votes)
Implementing DCT on Image (2D DCT) in C# and its Inverse
Introduction
A discrete cosine transform (DCT) expresses a sequence of finitely many data points in terms of a sum of cosine functions oscillating at different frequencies. DCTs are important to numerous applications in science and engineering, from lossy compression of audio and images (where small high-frequency components can be discarded), to spectral methods for the numerical solution of partial differential equations. The use of cosine rather than sine functions is critical in these applications: for compression, it turns out that cosine functions are much more efficient (as explained below, fewer are needed to approximate a typical signal), whereas for differential equations the cosines express a particular choice of boundary conditions.
In particular, a DCT is a Fourier-related transform similar to the discrete Fourier transform (DFT), but using only real numbers. DCTs are equivalent to DFTs of roughly twice the length, operating on real data with even symmetry (since the Fourier transform of a real and even function is real and even), where in some variants the input and/or output data are shifted by half a sample. There are eight standard DCT variants, of which four are common.
Background
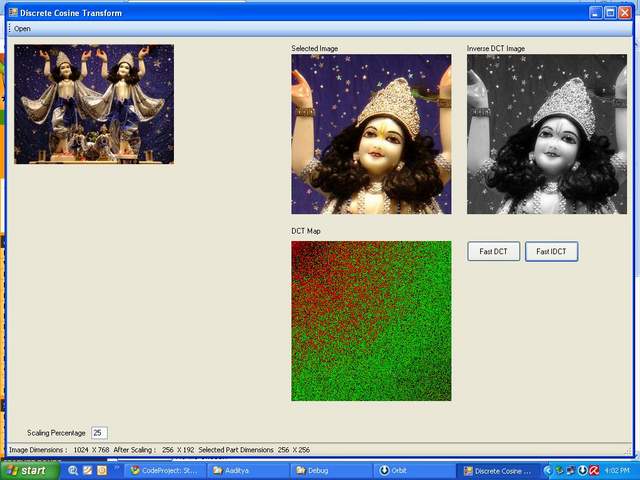
Here I am showing an implementation of 2D DCT. We generate the 2D DCT kernel first and then using matrix operations we perform DCT. I am very lazy to write the theory. Please refer to the proper books for the same.
Using the Code
Here we perform the following activities:
- Select the image, scale the image so that it fits the picture box, this scaling is shown in Scaling percentage box.
- Select a specific part of the image, we select image part of dimensions multiple of 2 (128*128, 256*256).
- Read the image in 2D Array, we are using pointer arithmetic for this, we have to allow pointer operations in project properties.
private void ReadImage() { int i, j; GreyImage = new int[Width, Height]; //[Row,Column] Input = new double [Width, Height]; //[Row,Column] Bitmap image = Obj; BitmapData bitmapData1 = image.LockBits(new Rectangle (0, 0, image.Width, image.Height), ImageLockMode.ReadOnly, PixelFormat.Format32bppArgb); unsafe { byte* imagePointer1 = (byte*)bitmapData1.Scan0; for (i = 0; i < bitmapData1.Height; i++) { for (j = 0; j < bitmapData1.Width; j++) { GreyImage[j, i] = (int)((imagePointer1[0] + imagePointer1[1] + imagePointer1[2]) / 3.0); Input [j,i]=(double)GreyImage[j,i]; //4 bytes per pixel imagePointer1 += 4; }//end for j //4 bytes per pixel imagePointer1 += bitmapData1.Stride - (bitmapData1.Width * 4); }//end for i }//end unsafe image.UnlockBits(bitmapData1); return; } - Create Object of
FastDCT2Dclass, which implements the DCT. - To find DCT, first we have to generate 2D DCT kernel and then implement multiplication:
public double[,] GenerateDCTmatrix(int order) { int i, j; int N; N = order; double alpha; double denominator; double[,] DCTCoeff = new double[N, N]; for (j = 0; j <= N - 1; j++) { DCTCoeff[0, j] = Math.Sqrt(1 / (double)N); } alpha = Math.Sqrt(2 / (double)N); denominator = (double)2 * N; for (j = 0; j <= N - 1; j++) for (i = 1; i <= N - 1; i++) { DCTCoeff[i, j] = alpha * Math.Cos(((2 * j + 1) * i * 3.14159) / denominator); } return (DCTCoeff); }public void FastDCT() { double[,] temp = new double[Width, Height]; DCTCoefficients = new double[Width, Height]; DCTkernel = new double[Width, Height]; DCTkernel = GenerateDCTmatrix(Order); temp = multiply(DCTkernel, Input); DCTCoefficients = multiply(temp, Transpose(DCTkernel)); DCTPlotGenerate(); return; }
Points of Interest
DCT plot is also generated using Dynamic Range Compression.
History
This is my first attempt. I have also added a slow version of DCT in the code, which is given by another author. Any changes or suggestions are welcome.
