Customizable Butterworth Digital Filter
4.94/5 (9 votes)
Filter specified by the pass frequency, stop frequency, passband attenuation, and stopband attenuation
Introduction
Most of the information necessary to implement digital filters is given in the well-known internet text "Cookbook formulae for audio EQ biquad filter coefficients" by Robert Bristow-Johnson [2001?]. Unfortunately, some important details are not explained in that document. The formulae are given in terms of a corner frequency f0. This is the frequency at which energy will be reduced by a half, which is neither the frequency to preserve nor the frequency to eliminate, but somewhere in the transition band in between. The cookbook formulae also require that the quality Q be specified, but do not explain how to choose Q.
The present article will answer both these unknowns. A Butterworth low-pass filter will be developed following the design guidelines given by [Stensby, 2005]. A few simple changes will result in a high-pass filter. Using both a low-pass filter and a high-pass filter results in a bandpass filter. Subroutine bfilt acts as either a low-pass filter or high-pass filter, depending on whether the requested passband frequency is less than or greater than the requested stopband frequency.
Background
(For a theoretical treatment of the Butterworth filter, please see the codeproject article "Lowpass, Highpass, and Bandpass Butterworth Filters in C#")
A digital signal is a sequence of amplitudes measured at equally spaced times. Typically, this represents a sound, but it could be anything: the voltage measured by a radar system or a brain wave.
A digital filter modifies a signal by removing selected frequencies and leaving the other frequencies intact. Filters work in the time domain, so there is no need to take the Fourier transform of the signal.
The Transition Band
Before reducing the sample rate of a signal, it's important to run it through a low-pass filter to remove frequencies greater than one-half the new sample rate. Suppose you wanted to reduce the sample rate of some audio from 44,100 samples per second to 4,410 samples per second. Then the new maximum frequency will be half of that, 2,205 cycles per second. Ideally, you would like to keep everything below 2,205 Hz and reject everything above it. This is not quite achievable. Instead of having a perfectly sharp transition between what is kept and what is rejected, there is a transition band. This is the range of frequencies where energy gradually declines from the passband to the stopband.
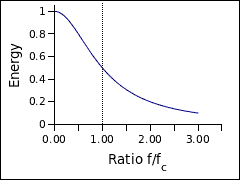
The above graph shows that at the cutoff frequency (f/fc = 1), half the energy passes through the filter.
Kinds of Filters
There are several kinds of digital filters, including Butterworth, Elliptical, and Chebyshev. The Butterworth filter is a popular choice because it has small attenuation in the passband, at the cost of a wide transition band. Butterworth filters come in different orders. The wide transition band can be made narrower by increasing the order.

The Equations
Given:
- fp
- frequency at the edge of the passband
- fs
- frequency at the edge of the stopband
- Hp
- minimum transmission in the passband
- Hs
- maximum transmission in the stopband
Find:
- fc
- the cutoff frequency
- n
- the order of the filter
For the low-pass filter, according to [Stensby, 2005],
$\epsilon = \sqrt{(\frac{1}{H_p})^2 - 1}$
$D = \frac{1}{H_s}$
$n = \frac{\log(\frac{\epsilon}{\sqrt{D^2-1}})}{\log(\frac{f_p}{f_s})}$
Choosing the cutoff frequency to meet the stopband specification and possibly exceed the passband specification:
$f_c = f_s \sqrt{D^2 - 1}^{\frac{-1}{n}}$
For the high-pass filter, make the simple modifications:
$n = \frac{\log(\frac{\epsilon}{\sqrt{D^2-1}})}{\log(\frac{f_s}{f_p})}$
$f_c = f_s \sqrt{D^2 - 1}^{\frac{+1}{n}}$
Next is the problem of choosing Q. According to [David S. 2010] :
Quote:About half way down [the Wikipedia page for Butterworth filter] is the table of "Factors of polynomials..." The 4 or 5 place numbers are 1/Q so their inverse is the number you are looking for.... In general any higher order filter shape can be split into a series of second order sections + one first order if an odd number is required. Each section will have its own Q and higher order filters will have a progression from low Q to high Q.
Wiki gives a formula for these numbers. There will be \(\frac{N}{2}\) passes through the filter and a sequence of \(\frac{N}{2}\) values. The required equation is thus:
$Q = \frac{-\frac{1}{2}}{\cos(\pi \frac{2 k + n - 1}{2 n})}$
where $k = \frac{N}{2} ... 1$
Now things are ready for the cookbook formulae. The main transform equation is:
Find the intermediate variables:
The coefficients for the low-pass filter are:
The coefficients for the high-pass filter are:
Using the code
The prototype for bfilt is:
int bfilt (double *s, int l, double fsamp,
double fpass, double fstop, double hpass, double hstop);
- s is an array containing the sample data
- l is the length of the array
- fsamp is the sample rate in samples per second
- fpass is the frequency of the passband edge in cycles per second
- fstop is the frequency of the stopband edge in cycles per second
- hpass is the minimum fraction transmitted in the passband, for example 0.99
- hstop is the maximum fraction transmitted in the stopband, for example 0.01
- A return value of zero means no errors.
Example Problem
The test program t_filt reads an audio file named input.raw. To keep things simple, the audio files must be mono, 16-bit integer samples, least-significant byte first, with no header. Here is some brief singing, recorded by TheScarlettWitch89 [2019]. Due to space limitations, you'll have to download this file from freesound and convert it yourself if you'd like to hear the results. Load the input in audacity and it produces the spectrogram: 
showing a main tone at around 400 cycles/second, with as many as 13 discernable overtones. The input is run through a low-pass filter and the result is written to lowpass.raw. The spectrogram is:

Frequencies above 1000 cycles/second have been filtered out. Next, the input is run through a high-pass filter and the result is written to highpass.raw. The spectrogram is:

Frequencies below 1000 cycles/second have been filtered out. Next, the input is run through a low-pass filter, and then a high pass filter, and the result is written to bandpass.raw. The spectrogram is:

Frequencies below 950 cycles/second and above 1050 cycles/second have been filtered out.
History
Revision 0 — 19 Sep 2021
References
- "Butterworth filter", on Wikipedia
- Website for program audacity
- "Cookbook formulae for audio EQ biquad filter coefficients", Robert Bristow-Johnson, [2001?], available from github
- "The Butterworth Low-Pass Filter", John Stensby, 19 Oct 2005, available from the University of Alabama
- "4th order Butterworth filter Q", forum comment by David S., 10 Nov 2010, at diyAudio
- "Female 'Ooh' Singing Voice", TheScarlettWitch89, 25 Feb 2019, at freesound
