DotNetMatrix: Simple Matrix Library for .NET
4.94/5 (57 votes)
A set of C# classes providing basic matrix operations
Introduction
The classes provided with this article give you a basic linear algebra package for .NET. It provides user-level C# classes for constructing and manipulating real, dense matrices. It is meant to provide sufficient functionality for routine problems, packaged in a way that is natural and understandable to non-experts. That said, it is simply a port of a public domain Java matrix library, called JAMA. Check the JAMA web site for more information.
Background
Currently, I work for a small GIS company here in Japan developing GIS components for application developers. Coordinate Transformation and therefore Affine Transformation is a very basic part of our development efforts. Recently, I was assigned a task of designing and implementing a new GIS system for the .NET framework with the ability to easily port to Java and other frameworks. I decided to make maximum use of matrix-based affine transformation, which is also a requirement of the OpenGIS Coordinate Transformation Specifications.
Then, I discovered that the Matrix class provided as part of the GDI+ in the .NET implements the affine transformations in a manner different from standard specifications. In short, while the standard 2D Coordinate System Affine Transformation Matrix is define as
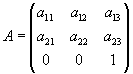
The matrix defined by GDI+ is
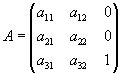
The effect is that most affine transformations with the GDI+ Matrix class will not conform to standard or specifications. For instance, by standard (and mathematically) anti-clockwise (or counter-clockwise) rotations are considered positive but must be negative when using the GDI+ classes.
To solve this problem, I decided to implement a standard affine transformation matrix and found this small Java general matrix library - JAMA. The classes presented with this article are ported from the JAMA with .NET specific improvements like operator overloading etc.
In a different article, I will discuss and present my affine transformation matrix, which should give the same effect (same properties and methods as the GDI+ Matrix class). The rest of the article is extracted from the JAMA documentation, and I will refer to the library as DotNetMatrix (the namespace).
Capabilities
DotNetMatrix is comprised of six C# classes: GeneralMatrix, CholeskyDecomposition, LUDecomposition, QRDecomposition, SingularValueDecomposition and EigenvalueDecomposition.
The GeneralMatrix class provides the fundamental operations of numerical linear algebra. Various constructors create Matrices from two dimensional arrays of double precision floating point numbers. Various gets and sets (properties) provide access to submatrices and matrix elements. The basic arithmetic operations include matrix addition and multiplication, matrix norms and selected element-by-element array operations. A convenient matrix print method is also included.
Five fundamental matrix decompositions, which consist of pairs or triples of matrices, permutation vectors, and the like, produce results in five decomposition classes. These decompositions are accessed by the GeneralMatrix class to compute solutions of simultaneous linear equations, determinants, inverses and other matrix functions. The five decompositions are
- Cholesky Decomposition of symmetric, positive definite matrices
- LU Decomposition (Gaussian elimination) of rectangular matrices
- QR Decomposition of rectangular matrices
- Eigenvalue Decomposition of both symmetric and nonsymmetric square matrices
- Singular Value Decomposition of rectangular matrices
The design of DotNetMatrix represents a compromise between the need for pure and elegant object-oriented design and the need to enable high performance implementations.
| Object Manipulation | constructors set elements get elements copy clone |
| Elementary Operations | addition subtraction multiplication scalar multiplication element-wise multiplication element-wise division unary minus transpose norm |
| Decompositions | Cholesky LU QR SVD symmetric eigenvalue nonsymmetric eigenvalue |
| Equation Solution | nonsingular systems least squares |
| Derived Quantities | condition number determinant rank inverse pseudoinverse |
Using the Code
The following simple example solves a 3x3 linear system Ax=b and computes the norm of the residual.
double[][] array = {{1.,2.,3},{4.,5.,6.},{7.,8.,10.}};
GeneralMatrix A = new GeneralMatrix(array);
GeneralMatrix b = GeneralMatrix.Random(3,1);
GeneralMatrix x = A.Solve(b);
GeneralMatrix Residual = A.Multiply(x).Subtract(b);
double rnorm = Residual.NormInf();
Points of Interest
There is an empty ISerializable interface implementation in all the classes. I do not know if serialization support is really needed, I could complete the implementations if needed.
License
This is basically a port of public domain codes, so the result is in the public domain.
History
- Jan 10, 2004 - initial release
Conclusion
Matrices are valuable mathematical tools which can be used to solve very complex problems, and coordinate transformation is no exception. The classes presented here can help you implement your own affine transformation classes to get a bit far than the .NET framework offers you. Also, since the classes are completely C# unlike the GDI+ classes, which are wrappers for a COM implementation, there is no interop overhead.
In my next article, I will present an affine transformation matrix class based on this library. Suggestions for improvements are welcomed.
