ZigZag Algorithm in a Grid (revised version, 2.1)
5.00/5 (5 votes)
Application to show how to zigzag order a matrix
Introduction
The downloadable code displays a grid of changeable size, rows and columns. The grid represents a matrix of numbers ordering by zigzag. It shows zero-based number indexing from zero to rows times columns minus one. If the matrix has 8 rows and 8 columns, the number indexing is from 0 to 63. It also shows red line segments across the numbers. The problem and why I have made this program follows: "How to serialize a matrix? That is: how to cast a two-dimensional array into a one-dimentional array? The most simple solution is to do a row-major or a column-major ordering. The more difficult part is to do zigzag ordering.
Background
The background of this problem is how e.g. image compression (JPEG) encodes and decodes blocks of frequency transformed images into a serialized stream (one-dimensional array). It is like a compromise between the row-major and column-major serialization.
Using the Code
This code snippet takes two arguments, rows count and columns count. Then generate a tuple list of zero-based indexing. (The language is C#.) The tuple consists of (0, 0), (0, 1), (1, 0), (2, 0), (1, 1) and so on...
private static Tuple<int, int>[] ZigZag(int rows, int cols)
{
Tuple<int, int>[] a = new Tuple<int, int>[rows * cols];
int p = 0;
int i = 0;
int j = 0;
a[p++] = Tuple.Create(i, j);
while (p < rows * cols)
{
if (j < cols - 1)
{
j++;
}
else
{
i++;
}
while (i < rows && j >= 0)
{
a[p++] = Tuple.Create(i, j);
i++;
j--;
}
i--;
j++;
if (i < rows - 1)
{
i++;
}
else
{
j++;
}
while (i >= 0 && j < cols)
{
a[p++] = Tuple.Create(i, j);
i--;
j++;
}
i++;
j--;
}
return a;
}
Here is the old version:
Drawing the 'ZigZag'-method:

Here is the new version:
Drawing the 'RowMajor'-method:

Drawing the 'ColumnMajor'-method:

Drawing the 'Random'-method:
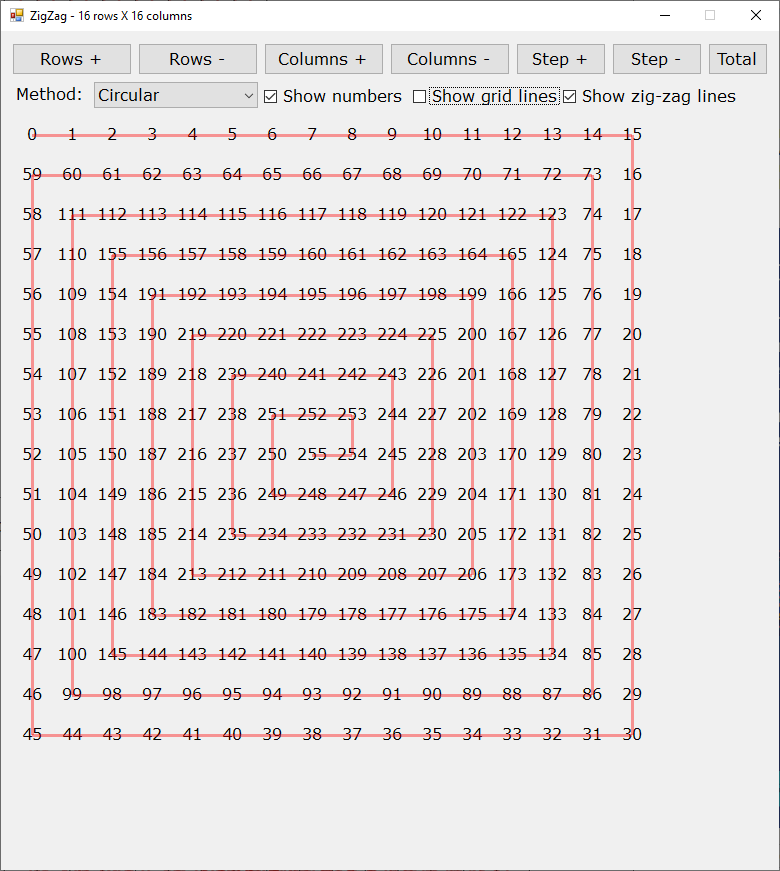
Drawing the 'Circular'-method:
Drawing the 'DiagonalUp'-method:

Points of Interest
The interesting part is to think strategic when designing the algorithm.
Test the program/problem for correctness. Find inconsistencies. Ask questions. Report errors.
History
First designed the algorithm, tested, made sure the numbers are correct back and forth.
Then made a visual application with user interaction (buttons and checkboxes) and a grid to display the numbers and zigzag line segments.
