Array-less Numerical Spiral Pattern
How to generate a spiral numerical pattern without using arrays

Introduction
The program comes from this question in the QA: Make pattern program in C#.
While the straightforward (and intuitive) solution uses an array to keep track of filled positions, the one presented here is array-less, achieving O(1), instead of O(N^2) space complexity.
The program source is already available on the linked page, here I am going to show the 'train of thought' leading to the algorithm.
The Idea
In order to provide an array-less solution, it is necessary to relate every number to its position on the screen, that is to find the mapping:
(x,y) -> n
where:
(x,y)is the coordinate, in a 'suitable' coordinate system, of the number in the pattern.nis the number itself.
Let's goto the details...
The Problem
Given a dimension (for instance 5), produce a spiral pattern, like the one shown in the following picture, on the console.
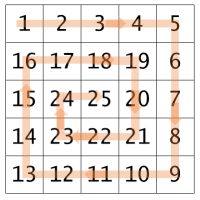
The Backward Problem
Consider now the following 'backward' problem:

It is, of course, pretty equivalent: solving the backward problem effectively solves the original one.
The Coordinate System
A 'suitable' (i.e., convenient) coordinate system is shown in pictures 3 and 4.


Such system is convenient because it highlights the symmetry of the system and applies nicely to both odd and even pattern dimensions.
It is worth noting the positions (blocks) of the numbers have:
- Even coordinates
.., -2, 0, 2, ..in odd-dimensions patterns (see the left part of picture 4) - Odd coordinates
.., -3, -1, 1, 3, ..in even-dimensions patterns (see the right part of picture 4)
The distance
In such a coordinate, a useful quantity is the distance, defined this way:
d(x,y) = max(abs(x), abs(y))
So that, for instance:
d(-3, 5) = 5d( 2, 2) = 2d( 2,-5) = 5
The Algorithm
Now, back to the backward algorithm (pardon the pun), let's try, for example, to find out how to assign the number 18 to position (4,-2).
The solution is counting the blocks up to the chosen coordinate, starting from the center, following the backward pattern.
Picture 5 shows clearly that there are two contributions:
- The inner square (yellow blocks)
- The partial ring (orange blocks)
Computing the inner square contribution is trivial: (D-1)^2 blocks (where D = d(4,-2) = 4 is the distance).


The partial ring contribution is more difficult. There can be four cases, depending on the position (see pictures 7,8):
- Case A: 'somewhere at the bottom'
- Case B: 'somewhere at the top'
- Case C: 'somewhere on the left'
- Case D: 'somewhere on the right'


The formula for such cases are shown in the following snippet:
public static int ring_contribution(int d, int x, int y)
{
if (y == -d)
return (d - 1) + (d + x) / 2; // Case A, somewhere in the bottom
else if (y == d)
return (d - 1) + 2 * d + (d - x) / 2; // Case B, somewhere in the top
else if (x == -d)
return (d - y) / 2 - 1; // Case C, somewhere in the left
else
return 2 * d + (d + y) / 2 - 1; // Case D, somewhere in the right
}
Adding the inner square and the partial ring contributions gives the expected result for the backward problem and, in turn, for the original one.
Points of Interest
Not useful a bit, I believe. Beating (again) the dead horse was some fun for me, though.
History
- 19th November, 2018 - First release
