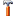/scrshot.JPG)
Introduction
MFC provides many functions to draw basic shapes, such as rectangle, ellipse, polygon, etc. It’s just a piece of cake. Also, a rectangle rotated 45 degrees can be drawn easily after doing a little math. But what if we want to rotate these shapes to a weird angle, say 11 degrees? Or we want to rotate an ellipse by 37 degrees?
Use SetWorldTransform() can free you from all the mathematics.
Details
First of all, let’s review the definition of rotation: the rotation performs a geometric transform which maps the position (x1, y1) of a picture element in an input image onto a position (x2, y2) in an output image by rotating it through a user-specified angle q about an origin (x0, y0).
The formula is:
x2 = cos(q)*(x1-x0) – sin(q)*(y1-y0) + x0;
y2 = sin(q)*(x1-x0) + cos(q)*(y1-y0) + y0;
where (x0, y0) are the coordinates of the center of rotation (in the input image) and q is the angle of rotation with clockwise rotations having positive angles.
Note here that we are working in image coordinates, so the y axis goes downward. With the above formulas in mind, let’s check what SetWorldTransform() can do for us.
From MSDN, it’s said that using SetWorldTransform(), for any coordinates (x, y) in world space, the transformed coordinates in page space (x’, y’) can be determined by the following algorithm:
x’ = x * eM11 + y * eM12 + eDx;
y’ = x * eM12 + y * eM22 + eDy;
Compare these two groups of formulas, we can get the correct values for parameter xform:
xform.eM11 = cos(q);
xform.eM12 = sin(q);
xform.eM21 = -sin(q);
xform.eM22 = cos(q);
xform.eDx = x0 – cos(q)*x0 + sin(q)*y0;
xform.eDy = y0 – cos(q)*y0 - sin(q)*x0;
That’s all the myth. Included is a simple project to demonstrate it.
License
This article has no explicit license attached to it, but may contain usage terms in the article text or the download files themselves. If in doubt, please contact the author via the discussion board below.
A list of licenses authors might use can be found here.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 








 10Q.
10Q.